Engineering Mathematics-II 1.0.4

per Huawei P20

Note, quiz, blog e video di matematica ingegneristica. IIa quasi copre argomenti importanti in capitolo

Capitolo 1 Serie di Fourier

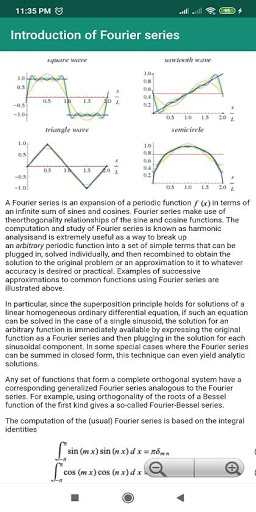
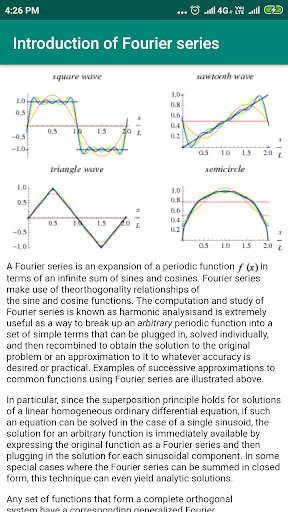
1. Introduzione della serie di Fourier
2. Serie di Fourier per funzioni discontinue
3. Convergenza delle serie di Fourier
4. Serie di Fourier per la funzione pari
5. Serie di Fourier per funzioni dispari
6. Serie a mezzo raggio
7. Trasformata di Fourier
8. Trasformazione seno e coseno

Capitolo 2 Trasformata di Laplace

1. Introduzione di Laplace Transform
2. Trasformazione di Laplace delle funzioni elementari
3. proprietà di Trasformata di Laplace
4. Modifica della proprietà della scala
5. seconda proprietà di spostamento
6. Trasformata di Laplace della derivata
7. Trasformata inversa di Laplace e sue proprietà
8. Teorema della convoluzione
9. Applicazioni di LT per risolvere le equazioni differenziali ordinarie

Capitolo 3 Equazione differenziale lineare del secondo ordine con coefficienti variabili

1. Metodi è noto un integrale
2. rimozione della prima derivata
3. modifica della variabile indipendente e variazione del parametro
4. Soluzione per metodo di serie

Capitolo 4 Equazione differenziale parziale lineare e non lineare del primo ordine

1. Formulazione di equazioni differenziali alle derivate parziali
2. soluzione dell'equazione mediante integrazione diretta
3. Equazione lineare di Lagrange
4. Metodo del carnet
5. Equazione differenziale parziale lineare di secondo e ordine superiore
6. Differenza parziale omogenea lineare e non omogenea
7. equazione dell'ennesimo ordine con coefficienti costanti
8. Separazione del metodo variabile per la soluzione delle equazioni di onda e calore

Capitolo 5 Calcolo vettoriale

1. Differenziazione dei vettori
2. funzione scalare e vettoriale
3. significato geometrico del gradiente
4. unità vettoriale normale e derivata direzionale
5. interpretazione fisica di divergenza e arricciatura
6. Integrale di linea
7. integrale di superficie e integrale di volume
8. Teorema di Green
9. I teoremi di divergenza di Stoke e Gauss. Qui dichiariamo che le informazioni non saranno da noi parti come a terzi.